Uji Perkiraan Klasik Regresi: Pola Perkara Uji Normalitas + Analisis

Dalam melaksanakan uji regresi linier berganda, maka suatu  penelitian harus melaksanakan dan memenuhi uji perkiraan klasik. Uji perkiraan klasik terdiri dari uji normalitas, uji multikolinearitas, uji autokorelasi, uji heteroskedastisitas. Di pos ini saya akan membahas uji normalitas dan analisisnya. 

Uji normalitas bertujuan untuk mengetahui distribusi normal dari variabel terikat (dependen) dan variabel bebas (independen) dalam model regresi. Uji normalitas bertujuan untuk menguji apakah dalam model regresi, variabel pengganggu atau residual terdistribusi normal atau mendekati normal. Model regresi yang baik yakni model yang mempunyai distribusi data yang normal atau mendekati normal. Untuk mengetahui signifikansi data yang terdistribusi normal, maka uji normalitas dilakukan memakai uji Kolmogorov Smirnov (K-S).

Contoh Kasus Uji Normalitas

Seperti pola soal uji regresi linier berganda sebelumnya yang sanggup anda lihat disini: Uji Regresi: Contoh Soal Regresi Linier Berganda + Analisis - Bagian I dan Uji Regresi: Contoh Soal Regresi Linier Berganda + Analisis - Bagian II, telah didapat variabel dependen Tingkat Penjualan dan Variabel Independen Biaya Produksi, Biaya Promosi dan Biaya Distribusi. Sekarang kita akan menguji apakah uji tersebut memenuhi uji perkiraan normalitas (menggunakan uji Kolmogorov Smirnov) ?

Langkah-langkah Pengujian

1. Pilih menu Analyze --> NonParametrics Test --> 1-Sample K-S, menyerupai pada tampilan berikut.

(Klik gambar untuk memperbesar)

2. Pada  layar akan muncul One-Sample Kolmogorov-Smirnov Test.

Ø  Pada serpihan Test Variable List isikan variabel dependen (Tingkat Penjualan) dan Variabel Dependen (Baya Produksi, Biaya Promosi dan Biaya Distribusi).

Ø  Pada serpihan Test Distribution pilih Normal.

3. Klik OK. Maka akan muncul output Kolmogorov Smirnov. Perhatikan output dibawah ini:

Untuk melihat normal tidaknya data memakai uji Kolmgorov Smirnov, maka sanggup dilihat pada serpihan Asymp Sig (2-tailed). Uji Kolmogorov-Smirnov mempunyai anutan untuk pengambilan keputusan sebagai berikut:

a.    Jika nilai signifikansi atau nilai probabilitas < 0.05, maka distribusi yakni tidak normal.

b.    Jika nilai signifikansi atau nilai probabilitas > 0.05, maka distribusi yakni normal.

Dari output diatas, terlihat bahwa nilai signifikansi Asymp.Sig 2-tailed pada masing-masing variabel adalah:

Ø  Signifikansi Tingkat Penjualan sebesar 0.786

Ø  Signifikansi Biaya Produksi sebesar 0.908

Ø  Signifikansi Biaya Distribusi sebesar 0.872

Ø  Signifikansi Biaya Promosi sebesar 0.663

Karena nilai signifikansi pada setiap variabel diatas 0,05, maka data dalam penelitian pada setiap variabel terdistribusi secara normal. Dengan kata lain, model regresi sanggup dikatakan memenuhi uji normalitas atau data dalam penelitian terdistribusi normal yang mengindikasikan bahwa model regresi layak digunakan untuk prediksi Tingkat Penjualan menurut pada masukan sejumlah variabel independennya.

Uji Tambahan Normalitas --> Histogram dan Probability Plot 

Selain memakai uji Kolmogorov Smirnov (K-S), ada pula uji perhiasan yang sanggup dilakukan untuk uji normalitas, yaitu memakai HISTOGRAM dan NORMAL PROBABILITY PLOT.  

1)    Langkah pertama yakni munculkan Unstandardized Residual

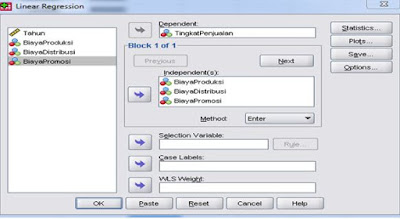
Pilih Analiyze --> Regression --> Linear

2)    Masukkan variabel dependen ke kotak Dependent dan variabel independent ke kotak Independent. Dalam hal ini variabel dependen yakni Tingkat Penjualan dan variabel independen yakni Biaya Produksi, Biaya Distribusi, dan Biaya Promosi.

Lihat Tampilan dibawah ini

3. Tekan  tombol Plots. Lalu aktifkan pilihan Histogram dan Normal Probability Plot:

4. Abaikan bagian lain, lalu tekan Continue dan klik OK. Maka akan muncul output histogram dan normal probability plot menyerupai gambar dibawah ini: 

Untuk mendeteksi apakah suatu penelitian memenuhi perkiraan normalias, maka maka sanggup dilihat pada grafik histogram. Data terdistribusi normal jikalau kurva normal yang berada di grafik mengikuti bentuk bel (lonceng). Dari grafik diatas terlihat bahwa sebaran data mempunyai kurva yang berbentuk lonceng. Karena itu error model regresi sanggup dikatakan berdistribusi normal.

Deteksi uji normalitas sanggup dilihat pada penyebaran data (berupa titik atau dot) pada sumbu diagonal dari grafik. Dasar pengambilan keputusan:

Ø  Jika data menyebar di sekitar garis diagonal dan mengikuti arah garis diagonal, maka model regresi memenuhi perkiraan Normalitas.

Ø  Jika data menyebar jauh dari garis diagonal dan/atau tidak mengikuti arah garis diagonal, maka model regresi tidak memenuhi perkiraan  Normalitas.

Dari grafik di atas, terlihat adanya titik-titik (dot) yang menyebar di sekitar garis diagonal dan penyebarannya mengikuti arah garis diagonal. Maka sanggup disimpulkan bahwa model regresi layak digunakan untuk prediksi Tingkat Penjualan menurut pada masukan sejumlah variabel independennya. Artinya model regresi tersebut memenuhi uji normalitas.

PERHATIKAN!!

Dalam melaksanakan uji normalitas, uji utama yang harus dilakukan yakni uji Kolmogorov Smirnov. Karena uji Kolmogorov Smirnov bersifat objektif (ketentuan pengujiannya memakai angka yang sudah pasti). Sedangkan uji Histogram dan Normal Probability Plot hanyalah sebagai uji perhiasan dalam uji normalitas, sebab pengujian memakai Histogram dan Normal Probability Plot sifatnya subjektif. Dikatakan subjektif sebab evaluasi memakai Histogram dan Normal Probability Plot sanggup menjadikan bias.

Sumber http://bahasekonomi.blogspot.com

Berlangganan Informasi Terbaru: