Cara Gampang Memahami Barisan Geometri
Apa kabar sobat BT? Dalam postingan kali ini kita akan membahas wacana Barisan Geometri atau biasa juga disebut dengan barisan ukur. Sebelumnya Om BT sudah pernah mempublish satu artikel wacana baris geometri ini (Baca : Rumus Barisan Geometri dan Contoh Soalnya). Nah untuk semakin memperjelas wacana bahasan dari barisan geometri ini Om BT kembali mempublish Cara Praktis Memahami Barisan Geometri. Semoga bermanfaat.
Sebelum kita bahas lebih jauh, sobat BT harus tahu dimana letak perbedaan antara barisan aritmatika dengan barisan geometri. Mengapa ini penting? yup, alasannya yaitu langkah pertama dalam menuntaskan soal-soal barisan dan deret yaitu sanggup membedakan bentuk barisannya. Barisan geometri, ataukah aritmatika. Keliru dalam membedakan, dijamin rumus yang sobat gunakan tidak tepat.
Dalam barisan aritmatika kita temukan bahwa suku berikutnya diperoleh dengan menambahkan suatu bilangan yang tetap (beda) dengan suku sebelumnya. Misalnya 1, 4, 7, 10,… (beda = 3)
Lain halnya dengan barisan geometri. Dalam suatu barisan geometri, suku selanjutnya diperoleh dengan mengalikan suatu bilangan tetap pada suku sebelumnya. Bilangan tetap itu disebut dengan rasio. Misalnya 2, 6, 18, 64,… (rasio =3)
Nilai rasio itu sendiri diperoleh melalui perbandingan tetap antara dua suku berturut-turut. Misal U2/U1 atau U3/U2 demikian seterusnya. Atau sanggup ditulis dengan bentuk umum ibarat berikut ini:
Oke, sobat BT, hingga sini clear yah? Lanjut!
Rumus suku ke-n barisan geometri
Misalkan suatu barisan geometri dituliskan dalam bentuk ibarat dibawah ini
Contoh:
1. Tentukan suku ke-15 dari barisan geometri 4, 8, 16, …
Jawab :
2. Suatu jenis basil berkembangbiak dengan cara membelah diri. Apabila setiap 6 menit basil membelah diri menjadi 3. Tentukan banyaknya basil dalam tabung tersebut sehabis berkembangbiak selama satu 1 jam kalau diketahui jumlah basil dalam tabung mula-mula 50 bakteri?
Jawab :
Diketahui
Jumlah basil mula-mula = U1 = 50
Rasio = 3
1 jam = 60 menit. Setiap basil membelah setiap 6 menit. Itu artinya, dalam satu jam, basil membelah diri sebanyak 10 kali. Jika setiap kali basil membelah diri dituliskan dalam satu bentuk barisan, maka tedapat 11 suku. Mengapa? Karena terhitung dengan suku pertama atau jumlah basil mula-mula ditambah dengan 10 kali membelah (10 + 1 = 11)
Jadi, jumlah basil sehabis berkembangbiak selama 1 jam yaitu 236.196 bakteri.
Gimana sobat BT? Belajar barisan geometri gampang bukan. Sampai ketemu di postingan-postingan Om BT selanjutnya. [bt]
Gimana sobat BT? Belajar barisan geometri gampang bukan. Sampai ketemu di postingan-postingan Om BT selanjutnya. [bt]
Sumber http://www.blogteknisi.com

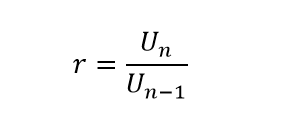








0 Response to "Cara Gampang Memahami Barisan Geometri"
Posting Komentar