Soal Dan Pembahasan Permutasi Dan Kombinasi
Pada kesempatan kali ini ID-KU akan memposting artikel wacana "Soal dan Pembahasan Permutasi dan Kombinasi ". Semoga beberapa pola di bawah ini sanggup membantu anda menuntaskan soal-soal yang terkait dengan permutasi dan kombinasi.Soal dan pembahasan permutasi
Contoh 1
Untuk menjabat pengelola suatu perusahaan memerlukan 3 staf pengurus yaitu ketua, sekretaris dan bendahara. Jika tersedia 7 calon, maka banyaknya susunan staf pengurus yang mungkin adalah...
A. 210 B.105 C.42 D.35 E.30
Pembahasan:
Jika susunan staf pengurus yakni ABC, maka A sebagai ketua, B sebagai sekretaris dan C sebagai bendahara. Tetapi bila susunan staf pengurus yakni CBA, maka C sebagai ketua, B sebagai sekretaris dan A sebagai bendahara. Kaprikornus terperinci bahwa ABC ≠ CBA. Ini berarti soal di atas memperhatikan urutan. Dengan demikian sanggup diselesaikan dengan cara permutasi. Pada soal diketahui bahwa akan dipilih 3 orang untuk menjadi staf pengurus dari 7 orang calon yang tersedia. ini berarti r = 3 dan n = 7. Hal ini merupakan permutasi 3 unsur dari 7 unsur. Dengan demikian banyaknya susunan pengurus yang mungkin adalah
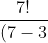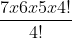
P (7,3) = !} "Soal dan Pembahasan Permutasi dan Kombinasi")
=
= 210
Contoh 2
Banyaknya susunan berbeda yang sanggup dibuat dari huruf-huruf pada kata "KALKULUS" adalah.....
A. 1.680 B.5.040 C.8.400 D.10.800 E.20.160
Pembahasan:
Kata KALKULUS terdiri dari 8 huruf, ini berarti n = 8
Pada kata KALKULUS terdapat abjad yang sama, yaitu:
Huruf K ada 2 maka r1 = 2
Huruf L ada 2 maka r2 = 2
Huruf U ada 2 maka r3 = 2
Banyaknya susunan abjad berbeda yang sanggup diperoleh ditentukan oleh rumus berikut.
P(8,2,2,2) =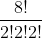
=
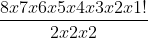
= 5.040
Jadi, banyaknya susunan abjad berbeda yang diperoleh yakni 5.040-->Jawaban:B
Contoh 3
Suatu keluarga yang terdiri atas 6 orang duduk mengelilingi sebuah meja makan yang berbentuk lingkaran. Berapa banyak cara biar mereka sanggup duduk mengeliingi meja makan dengan urutan yang berbeda?
A. 720 B. 120 C. 60 D. 30 E. 6
Pembahasan:
Banyaknya cara agar 6orang sanggup duduk menglilingi meja makan dengan urutan yang berbeda sama dengan banyak permutasi siklik (melingkar) 6 unsur yaitu:
(6 - 1)! = 5!
= 5 x 4 x 3 x 2 x 1
= 120 -----------> Jawaban: B
Soal dan pembahasan kombinasi
Contoh 4
Ada 5 orang dalam satu ruangan yang belum saling mengenal. Apabila mereka ingin saling berkenalan dengan berjabatan tangan sekali dengan setiap orang, maka banyaknya jabatan tangan yang terjadi adalah..
A. 5 kali
B. 10 kali
C. 15 kali
D. 20 kali
E. 25 kali
Pembahasan:
A berjabatan tangan dengfan B sama artinya dengan B berjabatan tangan dengan A. Dengan demikian AB = BA. Masalah ini sanggup diselesaikan dengan kombinasi. Pada soal diketahui ada 5 orang, sehingga n = 5. Karena untuk berjabatan tangan membutuhkan 2 orang, ini berarti r = 2. Banyaknya jabatan tangan sama dengan banyaknya kombinasi 2 unsur dari 5 unsur, yaitu:
C (5,2) =!)} "Soal dan Pembahasan Permutasi dan Kombinasi")
=
=
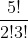
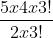
= 10
Jadi, banyaknya jabatan tangan yang terjadi yakni 10 kali-->Jawaban:B
Contoh 5
Di suatu perkumpulan akan dipilih perwakilan yang terdiri atas 6 orang. Calon yang tersedia 5 laki-laki dan 4 wanita. banyaknya susunan perwakilan yang sanggup dibuat bila sekurang-kurangnya terpilih 3 laki-laki adalah...
A. 84 B. 82 C. 76 D. 74 E. 66
Pembahasan:
Dari 5 laki-laki dan 4 perempuan akan dipilih 6 orang sebagai anggota perwakilan dengan ketentuan sekurang-kurangnya terpilih 3 pria. Ini berarti ada 3 macam susunan, yaitu:
1) 3 laki-laki dan 3 wanita,
2) 4 laki-laki dan 2 wanita,
3) 5 laki-laki dan 1 wanita
Susunan 1 (3 laki-laki dan 3 wanita)
Banyaknya cara menentukan 3 laki-laki dari 5 laki-laki yang ada yakni kombinasi 3 unsur dari 5 unsur, yaitu:
C (5,3) =!} "Soal dan Pembahasan Permutasi dan Kombinasi")
=
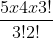
= 10
Banyaknya cara menentukan 3 perempuan dari 4 perempuan yang ada yakni kombinasi 3 unsur dari 4 unsur, yaitu:
C (4,3) =!} "Soal dan Pembahasan Permutasi dan Kombinasi")
=
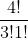
= 4
Dengan demikian banyaknya susunan yang terdiri dari 3 laki-laki dan 3 perempuan yakni 10 x 4 = 40
Susunan 2 (4 laki-laki dan 2 wanita)
Banyaknya cara menentukan 4 laki-laki dari 5 laki-laki yang ada yakni kombinasi 4 unsur dari 5 unsur, yaitu:
C (5,4) =!} "Soal dan Pembahasan Permutasi dan Kombinasi")
=
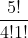
= 5
Banyaknya cara menentukan 2 perempuan dari 4 perempuan yang ada yakni kombinasi 2 unsur dari 4 unsur, yaitu:
C (4,2) =!} "Soal dan Pembahasan Permutasi dan Kombinasi")
=
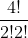
= 6
Dengan demikian bayaknya susunan yang terdiri atas 4 laki-laki dan 2 perempuan yakni 5 x 6 = 30
Susunan 3 (5 laki-laki dan 1 wanita)
Banyaknya cara menentukan 5 laki-laki dari 5 laki-laki yang ada yakni kombinasi 5 unsur dari 5 unsur, yaitu:
C (5,5) =!} "Soal dan Pembahasan Permutasi dan Kombinasi")
=
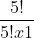
= 1
Banyaknya cara menentukan 1 perempuan dari 4 perempuan yang ada yakni kombinasi 1 unsur dari 4 unsur, yaitu:
C (4,1) =!} "Soal dan Pembahasan Permutasi dan Kombinasi")
=
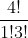
= 4
Dengan demikian bayaknya susunan yang terdiri atas 5 pria dan 1 perempuan yakni 1 x 4 = 4
Jadi, banyaknya susunan yang terdiri atas sekurang-kurangnya 3 laki-laki yakni 40+30+4 = 74
(Jawaban: D)
=
= 210
Contoh 2
Banyaknya susunan berbeda yang sanggup dibuat dari huruf-huruf pada kata "KALKULUS" adalah.....
A. 1.680 B.5.040 C.8.400 D.10.800 E.20.160
Pembahasan:
Kata KALKULUS terdiri dari 8 huruf, ini berarti n = 8
Pada kata KALKULUS terdapat abjad yang sama, yaitu:
Huruf K ada 2 maka r1 = 2
Huruf L ada 2 maka r2 = 2
Huruf U ada 2 maka r3 = 2
Banyaknya susunan abjad berbeda yang sanggup diperoleh ditentukan oleh rumus berikut.
P(8,2,2,2) =
=
= 5.040
Jadi, banyaknya susunan abjad berbeda yang diperoleh yakni 5.040-->Jawaban:B
Contoh 3
Suatu keluarga yang terdiri atas 6 orang duduk mengelilingi sebuah meja makan yang berbentuk lingkaran. Berapa banyak cara biar mereka sanggup duduk mengeliingi meja makan dengan urutan yang berbeda?
A. 720 B. 120 C. 60 D. 30 E. 6
Pembahasan:
Banyaknya cara agar 6orang sanggup duduk menglilingi meja makan dengan urutan yang berbeda sama dengan banyak permutasi siklik (melingkar) 6 unsur yaitu:
(6 - 1)! = 5!
= 5 x 4 x 3 x 2 x 1
= 120 -----------> Jawaban: B
Soal dan pembahasan kombinasi
Contoh 4
Ada 5 orang dalam satu ruangan yang belum saling mengenal. Apabila mereka ingin saling berkenalan dengan berjabatan tangan sekali dengan setiap orang, maka banyaknya jabatan tangan yang terjadi adalah..
A. 5 kali
B. 10 kali
C. 15 kali
D. 20 kali
E. 25 kali
Pembahasan:
A berjabatan tangan dengfan B sama artinya dengan B berjabatan tangan dengan A. Dengan demikian AB = BA. Masalah ini sanggup diselesaikan dengan kombinasi. Pada soal diketahui ada 5 orang, sehingga n = 5. Karena untuk berjabatan tangan membutuhkan 2 orang, ini berarti r = 2. Banyaknya jabatan tangan sama dengan banyaknya kombinasi 2 unsur dari 5 unsur, yaitu:
C (5,2) =
=
=
= 10
Jadi, banyaknya jabatan tangan yang terjadi yakni 10 kali-->Jawaban:B
Contoh 5
Di suatu perkumpulan akan dipilih perwakilan yang terdiri atas 6 orang. Calon yang tersedia 5 laki-laki dan 4 wanita. banyaknya susunan perwakilan yang sanggup dibuat bila sekurang-kurangnya terpilih 3 laki-laki adalah...
A. 84 B. 82 C. 76 D. 74 E. 66
Pembahasan:
Dari 5 laki-laki dan 4 perempuan akan dipilih 6 orang sebagai anggota perwakilan dengan ketentuan sekurang-kurangnya terpilih 3 pria. Ini berarti ada 3 macam susunan, yaitu:
1) 3 laki-laki dan 3 wanita,
2) 4 laki-laki dan 2 wanita,
3) 5 laki-laki dan 1 wanita
Susunan 1 (3 laki-laki dan 3 wanita)
Banyaknya cara menentukan 3 laki-laki dari 5 laki-laki yang ada yakni kombinasi 3 unsur dari 5 unsur, yaitu:
C (5,3) =
=
= 10
Banyaknya cara menentukan 3 perempuan dari 4 perempuan yang ada yakni kombinasi 3 unsur dari 4 unsur, yaitu:
C (4,3) =
=
= 4
Dengan demikian banyaknya susunan yang terdiri dari 3 laki-laki dan 3 perempuan yakni 10 x 4 = 40
Susunan 2 (4 laki-laki dan 2 wanita)
Banyaknya cara menentukan 4 laki-laki dari 5 laki-laki yang ada yakni kombinasi 4 unsur dari 5 unsur, yaitu:
C (5,4) =
=
= 5
Banyaknya cara menentukan 2 perempuan dari 4 perempuan yang ada yakni kombinasi 2 unsur dari 4 unsur, yaitu:
C (4,2) =
=
= 6
Dengan demikian bayaknya susunan yang terdiri atas 4 laki-laki dan 2 perempuan yakni 5 x 6 = 30
Susunan 3 (5 laki-laki dan 1 wanita)
Banyaknya cara menentukan 5 laki-laki dari 5 laki-laki yang ada yakni kombinasi 5 unsur dari 5 unsur, yaitu:
C (5,5) =
=
= 1
Banyaknya cara menentukan 1 perempuan dari 4 perempuan yang ada yakni kombinasi 1 unsur dari 4 unsur, yaitu:
C (4,1) =
=
= 4
Dengan demikian bayaknya susunan yang terdiri atas 5 pria dan 1 perempuan yakni 1 x 4 = 4
Jadi, banyaknya susunan yang terdiri atas sekurang-kurangnya 3 laki-laki yakni 40+30+4 = 74
(Jawaban: D)
0 Response to "Soal Dan Pembahasan Permutasi Dan Kombinasi"
Posting Komentar