Strategi Menduga Dan Menguji Kembali Dalam Matematika

Hallo temen-temen???
Pertama-tama gue ucapin trimakasih buat para pengunjung blog gue :). Slamat tiba di blog paling bermanfaat sedunia.
Dan gue doaian biar orang-orang yang ngunjungin blog gue pada masuk nirwana semua, trs selama hidupnya selalu di beri kemudahan, trs all the best deh buat kalian :D
Udah kaya ulang tahun aja ya ???.... Sorry ya klo penulis suka bercanda :)
Kembali lagi bersama gue muhamad pajar sidik, gue yakni seorang penulis blogger yang ganteng dan baik hati :D cieeee.....
Di hari yang indah ini alhamdulillah gue sanggup nulis artikel kembali, yang mudah-mudahan artikel ini sanggup bermanfaat buat kalian semua.
Kali ini gue bakalan nulis artikel wacana Strategi Menerka dan Menguji Kembali Dalam Matematika, Tanpa panjang lebar lagi yo check it out !

Strategi Menerka dan Menguji Kembali Dalam Matematika

Strategi Menerka dan Menguji Kembali Dalam Matematika merupakan seni administrasi yang pertama dalam pemecahan masalah. Ada 5 seni administrasi mengira dan menguji kembali dalam matematika, diantaranya yakni :

Memahami Soal
Menentukan Strategi
Melakukan Strategi
Melihat Kembali
Jika Perlu Gunakan Cara Lain

Supaya makin faham kita coba pelajari dalam teladan soal berikut ini :

Contoh Soal :

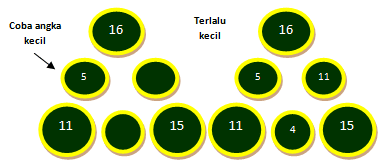
Pada diagram berikut isi bundar besar yakni jumlah bilangan yang terletak pada dua bundar kecil terdekat. Lengkapilah diagram kedua dengan hukum yang sama !!!

Jawaban :

1. Memahami Soal

Sebelum menuntaskan soal, kita mencoba memahami masalahnya. Dalam hal ini kita mencari bilangan a, b, c, sehingga :

memenuhi :

a + b = 16

b + c = 15

a + c = 11

2. Menentukan Strategi

Kita akan memakai strategi mengira dan menguji kembali.

3. Melakukan Strategi

Isi bundar kecil dengan 10, maka bundar di bab kanan harus diisi 6 dan terakhir dengan 9. Dengan Menguji kembali kita peroleh bahwa umlah 10 + 9 lebih besar dari 11. Oleh alasannya yakni itu terkaan kita terlalu besar, dan kita ganti dengan yang lebih kecil.

Mulai dengan 5 menghasilkan bilangan terlalu kecil, oleh alasannya yakni itu kita ganti dengan yang lebih besar. Kita sanggup mencoba dengan nilai tengah, misalkan 7 atau 8. Jika terlalu besar kita coba dengan terkaan awal sama dengan 6.

Kita sanggup melaksanakan perhitungan ini dan memperoleh hasil yang diinginkan.

4. Melihat Kembali

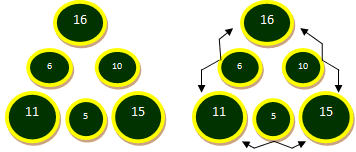
Jumlah bilangan di bundar besar yakni 16 + 11 + 15 = 42, sedangkan jumlah bilangan dilingkaran kecil yakni 6 + 10 + 15 = 21, yaitu setengah dari jumlah bilangan di bundar besar. Hal ini tidak mengejutkan alasannya yakni setiap bilangan di bundar kecil menyumbangkan dua kali ke jumlah bilangan di bundar besar.

5. Jika Perlu Gunakan Cara Lain

Kita mengetahui jumlah bilangan di bundar kecil yakni 21, setengah dari jumlah bilangan dilingkaran besar. Kita tahu pula bahwa a + b = 16, dengan demikian isi dari bilangan kecil yang ketiga yakni 21 - 16 = 5. Selanjutnya, isi bundar kecil sanggup ditentukan dengan cara yang biasa.

Contoh soal di atas mengambarkan bahwa dengan teknik yang tepat, soal sanggup diselesaikan dengan mudah. Tetapi cara ini diperoleh sehabis kita mencoba teknik yang sederhana. Selanjutnya, kalau dilihat kembali, kita seringkali akan menemukan teknik yang lebih baik.

Sekian artikel kali ini. Mohon maaf apabila ada salah-salah kata.
Saya sarankan baca artikel di bawah ini :

Akhir kata wassalamualaikum wr. wb.

Referensi :

Buku Olimpiade Matematika (Wono Setya Budhi Ph. D)
Sumber http://matematikaakuntansi.blogspot.com