5 Langkah Memilih Invers Matriks Ordo 3X3
Invers matriks yakni suatu nilai matriks yang dipangkatkan dengan -1. Namun dalam matriks operasi pangkat -1 ini tidak sesimple pada bilangan-bilangan biasa. Dalam matriks mempunyai hukum tersendiri untuk setiap oprasinya.
Berikut ini yakni 5 langkah memilih invers matriks ordo 3x3, diantaranya yakni :
- Tentukan minor matriks
- Tentukan kofaktor matriks
- Tentukan adjoin matriks
- Tentukan determinan matriks
- Operasikan rumus invers matriks
Untuk Menentukan minor matriks dapat dibaca selengkapnya pada link di bawah ini :
2. Tentukan kofaktor matriks
Untuk memilih kofaktor matriks dapat dibaca selengkapnya pada link di bawah ini :
3. Tentukan adjoin matriks
Untuk memilih adjoin matriks dapat dibaca selengkapnya pada link di bawah ini :
4. Tentukan determinan matriks
Untuk memilih determinan matriks dapat dibaca selengkapnya pada link di bawah ini :
5. Operasikan rumus invers matriks
Invers matriks mempunyai rumus sebagai berikut :
M-1 = (1/det(M)) x adj(M)
Keterangan :
M : Matriks
det : Determinan
adj : adjoin
Contoh :
Tentukan invers dari matriks dibawah ini !
Jawaban :
Untuk menjawab soalnya maka kita praktikan langkah-langkah di atas :
1. Tentukan minor matriks
Maka minor-minornya nya yakni :
a. Minor bari ke-1, kolom ke-1 :
5 x 9 - 8 x 6 = 45 - 48 = -3
b. Minor baris ke-1, kolom ke-2 :
9 x 4 - 7 x 6 = 36 - 42 = -6
c. Minor baris ke-1 kolom ke-3 :
4 x 8 - 5 x 7 = 32 - 35 = -3
d. Minor baris ke-2, kolom ke-1 :
2 x 9 - 3 x 8 = 18 - 24 = -6
e. Minor baris ke-2, kolom ke-2 :
1 x 9 - 3 x 7 = 9 - 21 = -12
f. Minor baris ke-2, kolom ke-3 :
1 x 8 - 2 x 7 = 8 - 14 = -6
g. Minor baris ke-3, kolom ke-1 :
2 x 6 - 3 x 5 = 12 - 15 = -3
h. Minor baris ke-3, kolom ke-2 :
1 x 6 - 3 x 4 = 6 - 12 = -6
i. Minor baris ke-3, kolom ke-3 :
1 x 5 - 2 x 4 = 5 - 8 = -3
Maka minor dari matriks A yakni :
2. Tentukan kofaktor matriks
sebab minornya sudah diketahui maka kita cari kofaktor matriks dari minor yang telah diketahui, maka :
Jawaban :
KEab = (-1)a+b x NEab
KE11 = (-1)1+1 x NE11 = (-1)2 x (-3) = 1 x -3 = -3
KE12 = (-1)1+2 x NE12 = (-1)3 x (-6) = -1 x (-6) = 6
KE13 = (-1)1+3 x NE12 = (-1)4 x (-3) = 1 x (-3) = -3
KE21 = (-1)2+1 x NE21 = (-1)3 x (-6) = -1 x (-6) = 6
KE22 = (-1)2+2 x NE22 = (-1)4 x (-12) = 1 x (-12) = -12
KE23 = (-1)2+3 x NE23 = (-1)5 x (-6) = -1 x (-6) = 6
KE31 = (-1)3+1 x NE31 = (-1)4 x (-3) = 1 x (-3) = -3
KE32 = (-1)3+2 x NE32 = (-1)5 x (-6) = -1 x (-6) = 6
KE33 = (-1)3+3 x NE33 = (-1)6 x (-3) = 1 x (-3) = -3
Maka kofaktornya yakni :
3. Tentukan adjoin matriks
Untuk memilih adjoinnya kita trasnposekan kofaktor matriksnya, maka adjoinnya yakni :

4. Tentukan determinan matriks
a = 1
b = 2
c = 3
d = 4
e = 5
f = 6
g = 7
h = 8
i = 9
DM ordo 3x3 = aei + bfg + cdh – bdi – afh – ceg
DM ordo 3x3 = (1 x 5 x 9) + (2 x 6 x 7) + (3 x 4 x 8) – (2 x 4 x 9) – (1 x 6 x 8) – (3 x 5 x 7)
DM ordo 3x3 = 45 + 84 + 96 – 72 – 48 – 105
DM ordo 3x3 = 0
Maka determinan dari matriks tersebut yakni 0
5. Operasikan rumus invers matriks
Pada langkah terakhir ini kita tinggal pribadi mengoperasikan rumus M-1 = (1/det(M)) x adj(M), sebab :
Sebenarnya matriks tersebut tidak mempunyai invers sebab pembaginya yakni 0. Penjelasan pola soal tersebut hanyalah polanya saja agar kalian memahami cara memilih invers matriks ordo 3 x 3.
Akhir kata wassalamualaikum wr. wb.
- Pengalaman berguru penulis
Sumber http://matematikaakuntansi.blogspot.com















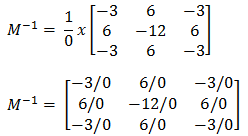
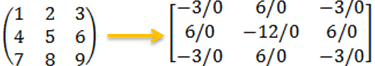





0 Response to "5 Langkah Memilih Invers Matriks Ordo 3X3"
Posting Komentar