Contoh Soal Ukuran Pemusatan Data (Mean, Median, Modus)
Contoh Soal Ukuran Pemusatan Data (Mean, Median, Modus) - kemampuan perihal teori/materi perlu diasah lebih lanjut dengan memperbanyak latihan menuntaskan permasalahan (soal-soal) yang berkaitan. Posting kali ini merupakan postingan lanjutan dari Ukuran Pemusatan Data (Mean, Median, Modus).
Mari senantiasa berguru bersama .
Contoh Soal Ukuran Pemusatan Data (Mean, Median, Modus)
Soal 1
Diberikan data nilai ulangan matematika dari 40 siswa berikut.
Sekian yang bisa kami sajikan dalam pembahasan tentang Contoh Soal Ukuran Pemusatan Data (Mean, Median, Modus) kali ini. Semoga apa yang kami berikan sanggup membantu anda. Nantikan selalu pembahasan-pembahasan menarik lainnya dari kami pada posting berikutnya tentunya seputar pembelajaran matematika. Salam Matematika !! Sumber http://www.partnermatematika.com
Mari senantiasa berguru bersama .
Contoh Soal Ukuran Pemusatan Data (Mean, Median, Modus)
Soal 1
Diberikan data nilai ulangan matematika dari 40 siswa berikut.
a. Sajikan kedalam tabel distribusi frekuensi berkelompok dengan batas bawah kelas pertama yaitu 65 dan panjang kelas 3.
b. Sajikan kedalam histogram.
Jawab:
a. Tabel distribusi frekuensi berkelompok nilai ujian matematika dengan bawah kelas pertama yaitu 65 dan panjang kelas 3.
Nilai | Frekuensi |
65 – 67 | 2 |
68 – 70 | 5 |
71 – 73 | 13 |
74 – 76 | 14 |
77 – 79 | 4 |
80 - 82 | 2 |
Jumlah |
b. Histogram
Soal 2
Nilai rataan hitung dari data berikut yaitu 34. Tentukan nilai p.
Nilai | Frekuensi | xi – xs |
21 – 25 | 2 | -15 |
26 – 30 | 8 | -10 |
31 – 35 | 9 | -5 |
36 – 40 | p | 0 |
41 – 45 | 3 | 5 |
46 – 50 | 2 | 10 |
Jawab:
diketahui nilai rataan hitung dari data di atas yaitu 34.
ditanyakan: nilai p?
Penyelesaian:
Nilai | Nilai tengah (xi ) | fi | di = xi – xs | fi . di |
21 – 25 | 23 | 2 | -15 | -30 |
26 – 30 | 28 | 8 | -10 | -80 |
31 – 35 | 33 | 9 | -5 | -45 |
36 – 40 | 38 | p | 0 | 0 |
41 – 45 | 43 | 3 | 5 | 15 |
46 – 50 | 48 | 2 | 10 | 20 |
Jumlah | 24 + p | -120 |
Berdasarkan tabel di atas terlihat bahwa rataan sementara (xs) yaitu 38, sebab xi – xs = 0.
Sesuai dengan rumus mean dengan memakai rataan sementara:
Soal 3
Diketahui kelas modus pada data berikut yaitu 51 – 60 dan nilai modusnya yaitu 56,5. Tentukan nilai c.
Nilai | Frekuensi |
31 – 40 | 2 |
41 – 50 | c |
51 – 60 | 12 |
61 – 70 | 10 |
Jawab:
Diketahui kelas modus pada data di atas yaitu 51 – 60 dan nilai modusnya yaitu 56,5.
Ditanyakan : nilai c ?
Penyelesaian:
Nilai | xi | fi |
31 – 40 | 35,5 | 2 |
41 – 50 | 45,5 | c |
51 – 60 | 55,5 | 12 |
61 – 70 | 65,5 | 10 |
kelas modus yaitu 51 – 60 dengan panjang kelas k = 10, frekuensi kelas modus f = 12. Sehingga diperoleh
tb = 50,5
d1 = 12 – c
d2 = 12 – 10 = 2
Modus data di atas dirumuskan dengan:
Soal 4
Tentukan median dari data tabel distribusi frekuensi berkelompok berikut.
Nilai | Frekuensi |
50 – 54 | 4 |
55 – 59 | 8 |
60 – 64 | 14 |
65 – 69 | 35 |
70 – 74 | 27 |
75 – 79 | 9 |
80 – 84 | 4 |
Jawab:
Penyelesaian:
Nilai Mat | Frekuensi (fi ) | Frekuensi Kumulatif (F) |
50 – 54 | 4 | 4 |
55 – 59 | 8 | 12 |
60 – 64 | 14 | 26 |
65 – 69 | 35 | 61 |
70 – 74 | 27 | 88 |
75 – 79 | 9 | 97 |
80 – 84 | 4 | 102 |
Jumlah | 101 |
Ukuran data pada Tabel tersebut yaitu 101 (ganjil), artinya median terletak antara datum ke-51. Datum tersebut terletak pada kelas 65 – 69.
Sekian yang bisa kami sajikan dalam pembahasan tentang Contoh Soal Ukuran Pemusatan Data (Mean, Median, Modus) kali ini. Semoga apa yang kami berikan sanggup membantu anda. Nantikan selalu pembahasan-pembahasan menarik lainnya dari kami pada posting berikutnya tentunya seputar pembelajaran matematika. Salam Matematika !!



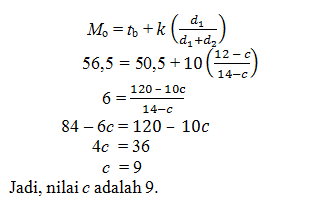

0 Response to "Contoh Soal Ukuran Pemusatan Data (Mean, Median, Modus)"
Posting Komentar