Garis-Garis Sejajar Dan Transversal
Garis-garis sejajar yakni garis-garis yang berada pada satu bidang dan tidak mempunyai titik potong. Perhatikan gambar di bawah ini.
 Gambar 1. Dua buah garis saling sejajar
Gambar 1. Dua buah garis saling sejajar
ditulis AB // CD berarti garis AB sejajar dengan garis CD.
Garis transversal yakni sebuah garis yang memotong dua buah atau lebih garis yang berada pada satu bidang dan mempunyai dua titik potong atau lebih.
Perhatikan gambar di bawah ini.

Gambar 2. Garis transversal t.
Garis t memotong garis AB di titik G dan CD di titik H. Garis t disebut sebuah garis transversal AB dan CD.
Ketika sebuah transversal memotong dua buah garis, pasangan-pasangan sudut istimewa akan terbentuk. Di bawah ini yakni penjelasannya.
Sudut-sudut saling sehadap
Perhatikan gambar di bawah ini.
 Gambar 3. Sudut-sudut saling sehadap.
Gambar 3. Sudut-sudut saling sehadap.

Sudut-sudut dalam berseberangan
Perhatikan gambar di bawah ini.
 Gambar 4. Sudut-sudut dalam berseberangan.
Gambar 4. Sudut-sudut dalam berseberangan.
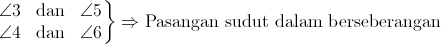
Sudut-sudut luar berseberangan
Perhatikan gambar di bawah ini.
 Gambar 5. Sudut-sudut luar berseberangan
Gambar 5. Sudut-sudut luar berseberangan

Sudut-sudut dalam sepihak
Perhatikan gambar di bawah ini.
 Gambar 6. Sudut-sudut dalam sepihak
Gambar 6. Sudut-sudut dalam sepihak

Sudut-sudut luar sepihak
Perhatikan gambar di bawah ini.
 Gambar 7. Sudut-sudut luar sepihak
Gambar 7. Sudut-sudut luar sepihak

Ketika dua buah garis yang saling sejajar dipotong oleh sebuah garis transversal maka akan terbentuk pasangan-pasangan sudut yang sama besar.
Sudut-sudut saling sehadap
Bila dua buah garis sejajar dipotong oleh sebuah transversal maka sudut-sudut yang saling sehadap akan sama besar. Perhatikan gambar di bawah ini.

Gambar 8. Sudut-sudut saling sehadap.
Buktikan bahwa:.gif)
Bukti:
garis AB dan CD saling sejajar. Salah satu garis misal CD digeser ke garis yang lain AB dengan kondisi garis transversal tetap maka.gif) akan sempurna menutup sudut
akan sempurna menutup sudut 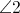.gif) .
.
maka terbukti .
.
Sudut-sudut dalam berseberangan
Bila dua buah garis sejajar dipotong oleh sebuah transversal maka sudut-sudut dalam berseberangan akan sama besar. Perhatikan gambar di bawah ini. 

Sudut-sudut luar berseberangan
Bila dua buah garis sejajar dipotong oleh sebuah transversal maka sudut-sudut luar berseberangan akan sama besar. Perhatikan gambar di bawah ini. 


Maka terbukti
Sudut-sudut dalam sepihak 


Sudut-sudut luar sepihak
Bila dua buah garis sejajar dipotong oleh sebuah transversal maka jumlah sudut-sudut luar sepihak akan sama dengan 180. Perhatikan gambar di bawah ini.
 Gambar 12. Sudut-sudut luar sepihak
Gambar 12. Sudut-sudut luar sepihak
Buktikan bahwa:
Bukti:


Sumber http://falensiocc.blogspot.com

ditulis AB // CD berarti garis AB sejajar dengan garis CD.
Garis transversal yakni sebuah garis yang memotong dua buah atau lebih garis yang berada pada satu bidang dan mempunyai dua titik potong atau lebih.
Perhatikan gambar di bawah ini.

Gambar 2. Garis transversal t.
Garis t memotong garis AB di titik G dan CD di titik H. Garis t disebut sebuah garis transversal AB dan CD.
Ketika sebuah transversal memotong dua buah garis, pasangan-pasangan sudut istimewa akan terbentuk. Di bawah ini yakni penjelasannya.
Sudut-sudut saling sehadap
Perhatikan gambar di bawah ini.


Sudut-sudut dalam berseberangan
Perhatikan gambar di bawah ini.

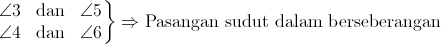
Sudut-sudut luar berseberangan
Perhatikan gambar di bawah ini.


Sudut-sudut dalam sepihak
Perhatikan gambar di bawah ini.


Sudut-sudut luar sepihak
Perhatikan gambar di bawah ini.


Ketika dua buah garis yang saling sejajar dipotong oleh sebuah garis transversal maka akan terbentuk pasangan-pasangan sudut yang sama besar.
Sudut-sudut saling sehadap
Bila dua buah garis sejajar dipotong oleh sebuah transversal maka sudut-sudut yang saling sehadap akan sama besar. Perhatikan gambar di bawah ini.

Gambar 8. Sudut-sudut saling sehadap.
Buktikan bahwa:
.gif)
Bukti:
garis AB dan CD saling sejajar. Salah satu garis misal CD digeser ke garis yang lain AB dengan kondisi garis transversal tetap maka
.gif) akan sempurna menutup sudut
akan sempurna menutup sudut 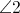.gif) .
.maka terbukti
 .
. Sudut-sudut dalam berseberangan
Bila dua buah garis sejajar dipotong oleh sebuah transversal maka sudut-sudut dalam berseberangan akan sama besar. Perhatikan gambar di bawah ini.

Gambar 9. Sudut-sudut dalam berseberangan
Buktikan bahwa:
Bukti:
Buktikan bahwa:

Bukti:

Maka terbukti  .
.
 .
.Sudut-sudut luar berseberangan
Bila dua buah garis sejajar dipotong oleh sebuah transversal maka sudut-sudut luar berseberangan akan sama besar. Perhatikan gambar di bawah ini.

Gambar 10. Sudut-sudut luar berseberangan
Buktikan bahwa:
Bukti:
Buktikan bahwa:

Bukti:


Maka terbukti

Sudut-sudut dalam sepihak
Bila dua buah garis sejajar dipotong oleh sebuah transversal maka jumlah sudut-sudut dalam sepihak akan sama dengan 180. Perhatikan gambar di bawah ini.

Gambar 11. Sudut-sudut dalam sepihak
Buktikan bahwa:
Bukti:
Buktikan bahwa:

Bukti:


Maka terbukti 

Sudut-sudut luar sepihak
Bila dua buah garis sejajar dipotong oleh sebuah transversal maka jumlah sudut-sudut luar sepihak akan sama dengan 180. Perhatikan gambar di bawah ini.

Buktikan bahwa:

Bukti:


Maka terbukti 

-Selamat belajar, Tuhan memberkati-
Sumber http://falensiocc.blogspot.com




0 Response to "Garis-Garis Sejajar Dan Transversal"
Posting Komentar