Cara Menghitung Simpangan Baku (Standar Deviasi)
Simpangan Baku – Varian dan standar deviasi (simpangan baku) merupakan ukuran-ukuran variasi yang sering digunakan oleh semua orang. Ini merupakan Standar deviasi (simpangan baku) dari akar kuadrat varian yang sudah sangat lazim digunakan.
Itulah sebabnya apabila ada salah satu nilai diantara kedua ukuran tersebut sudah anda ketahui maka untuk nilai ukuran yang lain juga sanggup diketahui.
Penghitungan
Untuk memilih dasar penghitungan varian dan simpangan baku merupakan cita-cita untuk mengetahui variasi dari kelompok data.
Untuk sanggup mengetahui variasi suatu kelompok data yaitu mengurangi nilai data beserta rata-rata kelompok data tersebut, kemudian hasil semuanya gres dijumlahkan.
Hanya saja cara tersebut tidak sanggup digunakan lantaran balasannya akan selalu menjadi 0.

Supaya nanti balasannya tidak menjadi 0 yaitu dengan mengkuadratkan setiap pengurangan nilai data serta rata-rata kelompok data tersebut yang kemudian dilakukan penjumlahan. Dengan begitu hasil penjumlahan kuadrat (sum of squares) tersebut akan mempunyai nilai positif.

Nilai varian didapat dari pembagian hasil penjumlahan kuadrat (sum of squares) dengan ukuran data (n).

Meskipun demikian ketika diterapkan nilai varian tersebut bias untuk menduga varian populasi. Dengan menggunakan rumus-rumus diatas maka nilai varian populasi sanggup lebih besar dari varian sampel.
Supaya tidak bias ketika menduga varian populasi maka n sebagai pembagi penjumlahan kuadrat (sum of squares) harus diganti dengan n-1 (derajat bebas) sehingga nilai varian sampel mendekati varian populasi. Dengan begitu rumus varian sampel akan menjadi menyerupai dibawah ini:

Nilai varian yang diperoleh merupakan nilai yang berbentuk kuadrat. Seperti contohnya satuan nilai rata-rata ialah gram dengan begitu nilai varian ialah gram kuadrat. Untuk memperoleh nilai satuannya maka varian diakarkuadratkan biar balasannya standar deviasi (simpangan baku).

Supaya mempermudah dalam penghitungan maka rumus varian dan simpangan baku tersebut sanggup diturunkan :
Rumus varian :

Rumus standar deviasi (simpangan baku) :

Keterangan:
s2 = varian
s = standar deviasi (simpangan baku)
xi = nilai x ke-i
 = rata-rata
= rata-rata
n = ukuran sampel
Baca juga : Cara Menghitung Akar Kuadrat
Contoh Penghitungan :
Sebagai teladan contohnya dalam suatu kelas, tinggi tubuh beberapa orang siswa yang dijadikan sampel ialah sebagai berikut.
172, 167, 180, 170, 169, 160, 175, 165, 173, 170
Dari data tersebut diketahui bahwa jumlah data (n) = 10, dan (n – 1) = 9. Selanjutnya sanggup dihitung komponen untuk rumus varian.

Dari tabel diatas maka kita sanggup mengetahui :

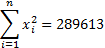

Apabila dimasukkan ke dalam rumus varian maka balasannya akan menyerupai dibawah ini
Dari penghitungan diatas sanggup diperoleh nilai varian sama dengan 30,32.
Dengan begitu cara mencari simpangan baku / standar deviasi sanggup dengan langkah mengakarkuadratkan nilai varian.

Source:
Rumus Standar Deviasi,simpangan baku,rumus simpangan baku,standar deviasi,cara menghitung simpangan baku,cara mencari simpangan baku,cara menghitung simpangan baku secara manual,contoh simpangan baku,rumus deviasi rata-rata,Rumus stan
Sumber https://caraharian.com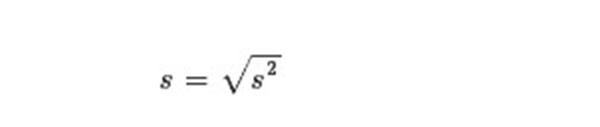

0 Response to "Cara Menghitung Simpangan Baku (Standar Deviasi)"
Posting Komentar