Cara Gampang Menghafal Rumus Trigonometri, Identitas, Jumlah Dan Selisih, Perkalian Lengkap

Oke deh...

Kita sudah mencar ilmu wacana rumus dasar trigonometri pada sudut segitiga

Kita juga sudah menelaah wacana sifat Sin-Cos-Tan tersebut  pada empat kuadran (I, II, III, dan IV)

Kita juga sudah mendalami abjad 'Trio Macan' itu (atau trio kwek-kwek juga boleh..he..he...) pada rumus jumlah dan selisih sudut.

Pastikan kalian sudah paham ketiga konsep di atas, kalau belum kalian bisa klik ketiga judul tersebut untuk mempelajarinya sebelum membahas rumus turunan yang banyaknya nauzubillaaah... :')

Oke..? Siap?

Ini rumus-rumusnya.....!

Ta..da...!

He..he..he..

Yang mau pengsan silahkan...

yang mau nggeblak.. nggih monggo ...

yang mau baku tinju.. jangan... hening mas...damai...he..he..

Pusing ya... gimana cara ngapalnya? rumusnya seabrek kayak gitu....!

Itulah yang saya pusingkan ketika dahulu kala... bahagia juga kalian bisa ikut merasakannya.. betapa empatinya kalian kepadaku.., jadi terharu... hiks...

Tapi.., tenang. Selalu ada jalan di setiap kesulitan. There is always a silver light in a cloudy sky...

Begini caranya...

Pertama.. rubah saja alpha dan beta menjadi A dan B. penyebutan alpha lebih ribet daripada A. agak lezat ngapalkannya. disamping itu A lebih bersahabat di pendengaran dan pengecap kita.

Dan..,

Sebenarnya, kesemua rumus itu berasal dari empat rumusan dasar jumlah dan selisih sudut di bawah ini.

Kalian sudah hafal kan? Kalau belum.. kalian bisa klik tautan ini.. di situ ada penjelasannya.

Untuk Tangens.., kerumitannya menciptakan saya lepas tangan dulu. ga ambil pusing...

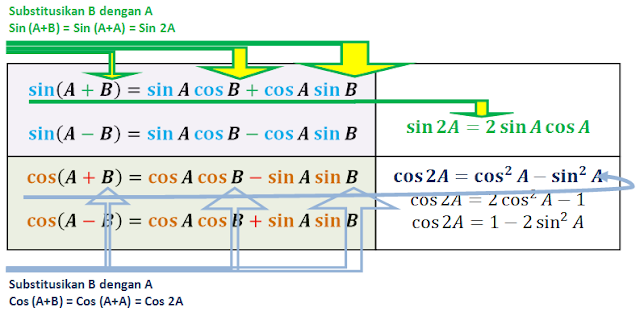
Rumus Sin 2A dan Cos 2A

Kita masuk ke Rumus Jumlah Sudut. Jika A = B, maka A akan saya masukkan ke semua lambang B yang ada di rumus. saya sederhanakan maka akan muncul menyerupai skema berikut.

Perhatikan hanya yang Sin(A+B) dan Cos (A+B), yang berturut-turut menjadi Sin 2A dan Cos 2A.

Dari sini kita dapatkan rumusan Sin 2A = 2 SinA CosA. Sin ini memang teratur, adil dan rapi...

dan kita juga dapatkan rumusan Cos 2A = Cos2 A - Sin2 A. Cos ni memang nyentrik.. bahagia betul menciptakan saya kesulitan karena susah buat angka pangkat di entri blog ini... hadeh...

Dan untuk Cos.. ada lagi turunannya. Yang mana, kalau kita sudah hafal dengan identitas

Sin2 A + Cos2 A = 1..(angka 2 itu kuadrat ya... maaf. keterbatasan), bahwasanya kita tidak harus menghafalkan dua rumusan ini.

Ya.. itu rumusan Sin 2A dan Cos 2A. Bagaimana dengan Tangens? Jika ada soal yang mengeluarkan Tangens, saya akan memecahnya menjadi Tan 2A = sin 2A/Cos 2A. Dengan begitu, saya selesaikan sin dan cos, kemudian sin saya bagi cos. Dengan begitu, saya tidak akan kehabisan space memory cuma untuk mengingat si doski yang sulit dipahami itu....

Di samping itu, dua 'cewek' yang bagus dan satunya nyentrik sudah cukuplah... nambah satu lagi malah bisa cakar-cakaran... wkwkwk 

Lanjut...

Sekarang kita kembali ke empat rumusan dasar.

Rumus Perkalian Trigonometri

Saya buat berbeda warna... variasi, biar kalian nggak bosen. he..he..

Saya akan menjumlahkan bab yang diblok warna ungu.. sampai nantinya cos A sin B 

dan -cos A sin B akan tereliminasi alias hilang... menyerupai skema berikut.

Ta..da...

Bagian ungu renta nampak ada tanda (+) berarti tempat itu merupakan hasil penjumlahan dari 2 persamaan di bawahnya. Kita mendapat sin (A+B) + sin (A-B) = 2 sinA cosB.

Hal yang sama saya lakukan terhadap cos.., di bab yang berwarna hijau. alhasil ialah sebagai berikut..

Praktis dipahami? coba perhatikan tanda silang merahnya.. di situ letak penyederhanaannya. Kita dapatkan CoCo De CoCo... cos(A+B) + cos(A-B)  =  2 cosA cosB

Oke.. kita lanjutkan lagi ya....

Kalau tadi ditambah, kini dikurangi. Saya tidak akan berbelit.., eksklusif ke hasilnya..

Ya.. alasannya ialah dikurang, semua tanda dari persamaan yang di bawah akan berubah. bisa kalian lihat ada tanda minus(-) merah di persamaan nomor dua baik di bab blok biru muda atau merah muda. 

Dan alhasil ialah sin(A+B) - sin(A-B) = 2 cosA sinB dan cos(A+B) - cos(A-B) = -2sinA sinB

Kita gabung hasil jerih payah kita menjadi tabel berikut...

Oke.. Jalan masih panjang. Kita akan menurunkan empat persamaan yang kita hasilkan menjadi bentuk berikut...

Di sini saya akan coba menjelaskan, bukan dengan kaidah penurunan rumus, namun hanya kaidah bagaimana cara mengingat rumusan itu. saya akan ambil pola pada sisi kanan atas, sehingga menjadi menyerupai  ini...

Perhatikan, bahwasanya bentuk umum kedua rumusan itu sama. 

Semua sin atau cos akan menjadi sin atau cos

Semua operasi hitung tambah atau kurang akan menjadi tambah atau kurang.

Semua A diubah menjadi (A+B)

Semua B diubah menjadi (A-B)

Angka 2 tetap menjadi angka 2

Perbedaannya hanya penambahan potongan 1/2 di rumusan turunannya. Tepatnya di depan (A+B) dan (A-B)

Ini berlaku untuk keempat rumusan di tabel itu...

Ya.. sejauh ini sudah 17 rumus kita telaah..

Ada baiknya kalian mahirkan dahulu penggunaan ketujuhbelas rumusan yang ada di atas. Jika kalian sudah mahir, kalian bisa menambah hafalan kalian dengan rumus trigonometri yang lain.

Coba dahulu menguji hafalan kalian dengan:

1. Tuliskan empat rumusan dasar jumlah/selisih sudut. (4rumusan)

2. Tuliskan kombinsi penjumlahan dan pengurangan rumusan (4 rumusan)

3. Tuliskan rumusan Sin 2A dan Cos 2A dengan mensubstitusi A ke B. (2 rumusan)

4. Substitusikan sin2 A + cos2 A = 1 ke hasil cos 2A pada nomor 3. (2 rumusan)

5. Turunkan bentuk rumusan di nomor 2 dengan mengganti A dan B menjadi (A+B) dan (A-B) serta mengalikan dengan 1/2 utk (A+B) dan (A-B) hasilnya.

Hafalkan prosesnya saja. Jika kalian sudah mampu., berarti hebat.. Selamat..!

Kita akan lanjutkan lagi di postingan yang lain.., masih ada beberapa rumus trigonometri yang siap menanti untuk kita hafalkan... Siap..?

Dan.. semua rumus itu akan saya gambarkan dalam satu lembar ukuran folio atau A4 semoga gampang mengurutkan dan menghafalkannya.. dan INI DIA... !

Sampai Jumpa...!

Selamat Belajar... dan tetap semangat..!

Sumber http://sekolah-matematika-sains.blogspot.com

Berlangganan Informasi Terbaru: