Soal Dan Pembahasan Persamaan Dan Pertidaksamaan Trigonometri

Pada kesempatan kali ini ID-KU akan memposting artikel wacana "Soal dan Pembahasan Persamaan dan Pertidaksamaan Trigonometri ". Semoga beberapa rujukan di bawah ini sanggup membantu anda menuntaskan soal-soal yang terkait dengan persamaan dan pertidaksamaan trigonometri.

Rumus-rumus Dasar Persamaan Trigonometri
1. sin x = sin α
         x₁ = α + k . 360⁰ atau x₂ = (180⁰ - α ) + k . 360⁰
2. cos x = cos α
          x = ± α + k . 360⁰
3. tan x = tan α
          x = α  + k . 180⁰
dengan k ∈ bilangan bulat

Persamaan trigonometri berbentuk a cos x + b sin x = c sanggup diselesaikan dengan terlebih dahulu mengubah bentuk persamaan itu menjadi bentuk:

 k cos (x - α ) = c  dengan k = $\sqrt{a^{2}+b^{2}}$

a cos x + b sin x = k cos (x - α) = c
dengan  k = $\sqrt{a^{2}+b^{2}}$ dan tan α = b/a

Syarat semoga persamaan a cos x + b sin x = c sanggup diselesaikan adalah:

c²  ≤ a² + b²

Pertidaksamaan trigonometri yakni sutu pertidaksamaan yang memuat fungsi-fungsi trigonometri. Himpunan penyelesaian suatu pertidaksamaan trigonometri akan gampang ditentukan jikalau memakai denah grafik fungsi trigonometri.

Contoh ❶
Himpunan penyelesaian dari pesamaan:
2sin x⁰ - √3 = 0, 0⁰ ≤ x ≤ 2π⁰ yakni .....
A. {π/3 , 2π/3}
B. {π/3 , π/6}
C. {π/3 , π/2}
D. {π/3 , 5π/6}
E. {2π/3 , 5π/6}

Pembahasan:
2sin x⁰ - √3 = 0
2sin x⁰ = √3
  sin x⁰ = (1/2)√3
  sin x⁰ = sin π/3⁰
       x₁ = π/3 + k . 360 atau x₂ = (π - π/3) + k . 360
Untuk k = 0 maka:
       x₁ = π/3
       x₂ = 2π/3
Jadi, himpunan penyelesaiannya yakni {π/3 , 2π/3} -----> Jawaban: A

Contoh ❷
Diketahui persamaan 2sin² x⁰ + 5sin x⁰ - 3 = 0 dan -π/2 < x < π/2. Nilai cos x =...
A. $-\frac{1}{2}\sqrt{3}$
B. $-\frac{1}{2}$
C. $\frac{1}{2}$
D. $\frac{1}{2}\sqrt{2}$
E. $\frac{1}{2}\sqrt{3}$

Pembahasan:
Misalkan sin x = y dan -π/2 < x < π/2 ⇛ Kuadran I dan kuadran IV
2sin² x + 5sin x - 3 = 0
⟺ 2y² x + 5y - 3 = 0
⟺ (y + 3)(2y - 1) = 0
⟺ y = -3  atau y = 1/2
⟺ sin x = -3 => (tidak memenuhi)
atau
⟺ sin x = 1/2
⟺ sin x = sin π/6
          x = π/6 + k . 360 atau x = (π - π/6) + k . 360
     Untuk k = 0 maka x = π/6
Jadi, cos π/6 = $\frac{1}{2}\sqrt{3}$ -----> Jawaban: E

Contoh ❸
Bentuk (√3 sin x⁰ - cos x⁰) sanggup diubah menjadi bentuk k cos (x - α)⁰ yaitu.....
A. 2cos (x - 30)⁰
B. 2cos (x - 60)⁰
C. 2cos (x - 120)⁰
D. 2cos (x - 150)⁰
E. 2cos (x - 210)⁰

Pembahasan:
a cos x⁰ + b sin x⁰ = k cos (x - α)⁰, dengan k = $\sqrt{a^{2}+ b^{2}}$ dan tan α=b/a
Diketahui √3 sin x⁰ - cos x⁰, berarti a = -1 dan b = √3
k = $\sqrt{a^{2}+ b^{2}}$ = $\sqrt{(-1)^{2}+ (\sqrt{3})^{2}}$ = 2
tan α = b/a = (√3)/(-1) = -√3
      α = 120⁰ (kuadran II, alasannya sinus konkret dan kosinus negatif)
Jadi, bentuk √3 sin x⁰ - cos x⁰ = 2cos (x - 120)⁰ -----> Jawaban: C

Contoh ❹
Tentukan batas-batas nilai p semoga persamaan 2p cos x + (p + 1)sin x = 3p+1 sanggup terselesaikan.
A. p ≥ -1
B. -1 < p < 0
C. -1 ≤ p ≤ 0
D. p ≤ -1 atau p ≥ 0
E. 0 < p < 1

Pembahasan:
Agar persamaan 2p cos x + (p + 1)sin x = 3p + 1 sanggup diselesaikan, maka:
(3p + 1)²      ≤ (2p)² + (p + 1)²
9p² + 6p + 1 ≤ 4p² + p² + 2p + 1
9p² + 6p + 1 ≤ 5p² + 2p + 1
4p² + 4p       ≤ 0
4p(p + 1)      ≤ 0

------> Jawaban: C



Contoh ❺
Himpunan penyelesaian persamaan sin x⁰ - √3 cos x⁰ = √2; 0⁰ < x < 360⁰ adalah..
A. {15, 285}
B. {75, 165}
C. {105, 195}
D. {165, 225}
E. {195, 285}

Pembahasan:
sin x - √3 cos x = √2 ; 0 < x < 360
k = $\sqrt{1^{2}+(\sqrt{-3})^{2}}$ = √4 = 2
tan α = 1/(-√3) = (-1/3)√3
      α = 150⁰ (kuadran II)
Persamaannya diubah menjadi bentuk:
2 cos (x - 150) = √2
cos (x - 150) = (1/2)√2
cos (x - 150)⁰ = cos 45⁰
      (x - 150)⁰ = 45⁰ + k . 360
                 x⁰ = 195⁰ + k . 360⁰
untuk k = 0, maka x⁰ = 195⁰
atau
      (x - 150)⁰ = -45⁰ + k . 360⁰
                 x⁰ = 105⁰ + k . 360⁰
untuk k = 0, maka x⁰ = 105⁰
Jadi, himpunan penyelesaiannya yakni {105⁰, 195⁰}---> Jawaban: C

Contoh ❻
Himpunan penyelesaian pertidaksamaan cos 2x⁰ - cos x⁰ > 0 untuk 0⁰ ≤ x ≤ 360⁰ adalah...
A. {x| 120⁰ < x < 240⁰}
B. {x| 0⁰ < x < 120⁰}
C. {x| 240⁰ < x < 360⁰}
D. {x| 120⁰ < x < 360⁰}
E. {x| 0⁰ < x < 210⁰}

Pembahasan:
cos 2x - cos x > 0
⟺ (2cos² x⁰ - 1) - cos x⁰ > 0
⟺ 2cos² x⁰ - cos x⁰ - 1 > 0
Misalkan cos x⁰ = y
Pembuat nol:
2y² - y - 1 = 0
(2y + 1)(y - 1) = 0
  y = -1/2 atau y = 1
cos x⁰ < -1/2 atau cos x⁰ > 1(tidak memenuhi)
Sketsa grafik fungsi y = cos x untuk 0⁰ < x < 360⁰ adalah








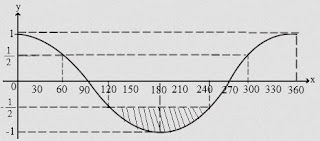
 Daerah yang memenuhi cos x⁰ < -1/2 terletak dalam interval 120⁰ < x < 240⁰. Jadi, himpunan penyelesaiannya yakni {x| 120⁰ < x < 240⁰}
----> Jawaban: A

Demikian postingan kali ini mudah-mudahan dari beberapa rujukan di atas sanggup membantu anda mengerjakan contoh-contoh lain terkait dengan persamaan dan pertidaksamaan trigonometri. 


Sumber http://ilmuku-duniaku14.blogspot.com

Berlangganan Informasi Terbaru: