Cara Gampang Mengurutkan Cuilan Berpenyebut Tidak Sama Dari Yang Terkecil Ke Terbesar
Hai.. ketemu lagi di sini... Kali ini saya akan menjelaskan beberapa cara dalam mengurutkan pecahan dengan penyebut yang berbeda dari teerkecil hingga terbesar yang cukup mudah, bahkan kalau pecahannya itu jumlahnya banyak...
Pastikan kalian baca hingga tamat ya.. alasannya yaitu cara mudahnya ada di cuilan akhir...
Oke kita lanjut..
Sebenarnya ada beberapa cara dasar untuk menuntaskan pengurutan bilangan pecahan ini.
Cara Pertama, dengan menyebabkan semua bilangan pecahan itu menjadi bilangan desimal.
Lalu diurutkan menurut bilangan desimal yang kite peroleh. Sebagaimana telah dicontohkan disini
Cara kedua, dengan menyamakan penyebut dari semua bilangan pecahan tersebut.
Cara ini dapat efektif kalau dilakukan pada hanya dua atau tiga bilangan pecahan. Namun sangat boros waktu untuk mengurutkan bilangan pecahan menyerupai soal saya ini.
Penyebut disamakan dulu menjadi
Pusing...?
He..he.. sabar..., saya akan coba permudah dengan mengurangi beban berat kita mengalikan begitu banyak angka itu.
Kemudahan pertama, jangan kalikan penyebutnya.., terperinci niscaya nilai mereka semua sama... Oke...?
Kemudahan kedua, mari kita kembali ke soal, dan kita pilah bilangan pecahan yang memusingkan kepala itu menjadi tiga bagian, yakni kurang dari setengah, antara setengah dengan satu dan lebih dari satu.
Lalu kita urutkan menjadi menyerupai ini
Nah.., kalau sudah begini. Kita lebih gampang mencari KPK penyebutnya. Bandingkan yang berwarna sama saja. Kita mulai dari yang mudah.., yang berwarna biru..
Menjadi...
hasilnya
Sekarang kita beralih ke cuilan berwarna merah...
Dengan cara yang sama.. kita modifikasi menjadi
Diolah lagi dengan mengalikan pembilang menjadi...
Sehingga... urutan yang telah kita susun di awal tadi sudah tepat. Yakni...
Bukan kebetulan... alasannya yaitu saya memakai cara satu lagi yang jaaauuuuuuuuuuhh lebih mudah.. he..he... penasaran?
Oke ... kita mulai lagi dari awal ya...?
Cara Ketiga, dengan mengalikan silang dan trial and error
Saya akan acak kembali menjadi menyerupai ini...
Pertama, pilih dua saja dari bilangan itu... dan kita kalikan silang.
Maksudnya menyerupai ini...
Lalu kita ambil satu bilangan lagi untuk diuji dimana posisi bilangan itu.. ambil acak saja....
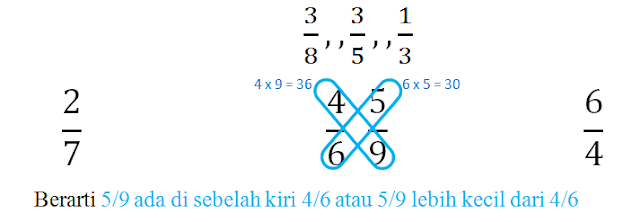
Berarti 4/6 di sebelah kanan 2/7. Dan di sebelah kiri 6/4
Menjadi menyerupai ini
Ambil satu lagi untuk kita dekatkan dengan 4/6. Saya pilih 5/9.
Ambil lagi satu.. saya pilih 1/3. Saya coba di sebelah kiri dulu... mengapa? Karena beliau kurang dari setengah (1/2). Kalau saya pilih di sebelah kanan dan saya cek dengan 6/4 alangkah banyak waktu terbuang untuk mengecek sesuatu yang tidak perlu. Kalau kalian sudah banyak berlatih sudah dapat punya insting ini.. he..he..
Pilihannya di sebelah kanan 2/7, atau kanan 5/9 atau kanan 4/6 atau kanan 6/4. Yang terakhir ga mungkin. Saya pilih di kanan 2/7 alasannya yaitu nilai 1/3 mendekati 2/7 (= 1/3,5).
Menjadi...
Saya tidak akan ngecek posisi 1/3 dengan 2/7, alasannya yaitu saya yakin 1/3 di sebelah kanan 2/7.. kalo ga percaya (dan sekalian latihan) coba kalian cek sendiri..
Hingga urutannya menjadi...
Kita ambil satu secara acak..., dan saya menentukan 3/8 berada di sebelah kiri 5/9, alasannya yaitu 3/8 kurang dari setengah dan 5/9 lebih dari setengah...
Namun disini saya akan mencoba meletakkan di posisi yang kurang tepat.. sekedar untuk mengambarkan bahwa di posisi manapun kita menempatkan bilangan yang akan kita uji, hasilnya akan benar.. kita memakai ‘insting’ matematika hanya untuk mempersingkat waktu dan tenaga saja..
Namun disini saya akan mencoba meletakkan di posisi yang kurang tepat.. sekedar untuk mengambarkan bahwa di posisi manapun kita menempatkan bilangan yang akan kita uji, hasilnya akan benar.. kita memakai ‘insting’ matematika hanya untuk mempersingkat waktu dan tenaga saja..
Saya letakkan 3/8 antara 2/7 dan 1/3
kita pindah menjadi
Berarti posisi 3/8 di sebelah kiri 5/9.
Posisi menjadi menyerupai ini...
Oke.. 3/5 itu kurang dari setengah, berarti PASTI ia ada di sebelah kanan 5/9 yang sedikit lebih kecil dari setengah(5/10). Dan saya menentukan di sebelah kanan 3/8 alasannya yaitu penyebut 3/5 lebih kecil. Ingat 3 jeruk dibagikan ke 5 orang porsi per orangnya akan lebih besar daripada 3 jeruk dibagikan ke 8 orang.
Namun, sekali lagi.., saya akan mencontohkan “pilihan yang kurang tepat, sekedar untuk menegaskan ulang, dimanapun pilihan kita, kita tetap on the track... :)
Saya pilih 3/5 berada di antara 2/7 dan 1/3..... pilihan yang paling stupid...!
Kita pindah 3/5 ke kanan 1/3... once again..., let’s make another mistake....!
Oops... salah lagi.. harusnya 3/5 disebelah kanan 3/8...
But it’s ok... there’s always a silver light in a cloudy sky...
He..he.. salah lagi....
Keep going.. it's getting closer and closer...
Yap... karenanya hingga juga...
Hasil karenanya adalah....
Ta..da...!
Kelihatannya mungkin usang yah... tapi kalau dilaksanakan di kertas coret-coretan luasnya ga lebih dari setengah jengkal kali setengah jengkal...!
Kalau ada yang berpikir ini terlalu panjang.., penyebabnya adalah... saya yang harus menjelaskan detail kalau sudah terbiasa, perkaliannya tinggal diawang saja... he..he.....
Dah hingga di sini dulu...
Tetap semangat belajar...
No need to worry about mistake..,
just do it again and again... you’ll improve your math’s skill...
See you on next SMS, Sekolah Matematika Sains...!



























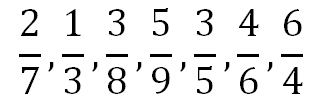
0 Response to "Cara Gampang Mengurutkan Cuilan Berpenyebut Tidak Sama Dari Yang Terkecil Ke Terbesar"
Posting Komentar